電動ガン

理想的な電動ガンを求めて

AEGにおいて、バレル長に応じた最適なシリンダ穴位置とピストン重量の組み合わせがあるはずなので、簡易なモデルを作り、運動方程式を解いて考えてみました。
簡易なモデルにしたのは力学の専門家ではないので理想的な方程式が立てられないこともあり、難解な空気の粘性に関する力は無視しています。また圧縮された空気の漏れも考慮していません。
もっと現実的な運動方程式が導ける方のご提案いただけましたら改善したいと思います。

以下の式は空気の密度変化による圧力を示した式で、断熱変化でκ=1.4 定熱変化でκ=1.0　となります。気体は圧縮すると温度が上がりますが、AEGでは完全に断熱されているわけではなく、シリンダ等に温度が逃げますので中間のκ=1.2にします。

ピストンの運動方程式

弾の運動方程式

二階連立常微分方程式の初期値問題になりますので初期値はスプリングが一番縮んでいる時点の時間をt=0とし、以下の初期値を与えます。

他の条件として

1-ピストンがシリンダ穴位置を通過するまで空気の圧縮はされないのでp=0

2-弾はHopパッキンを通過するまで動かないので、ピストンに圧縮された空気が弾を押す力がHopパッキン通過力を上回るまでr2=0

という条件をいれます。
この常微分方程式の数値解をRunge-Kutta法で求めます。
手持ちがPDWなので実際に各種測定をしてシュミレーションしてみました。弾質量m2=0.2[g]の場合とします。

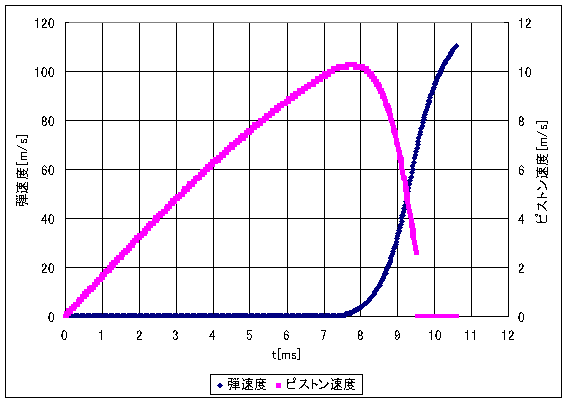
このグラフから動き出したピストンはシリンダ穴を越えるまでぐんぐん加速し7.2msで穴を通過し、シリンダ内圧を高めていきます。7.6msでHopパッキン通過力を超え、弾は加速して行きますがまだまだ圧力も上がって行きます。9.5msでピストンは前進端まで達し、圧力もここで最高点に達します。
驚いたことにこの時点で弾はわずか4cmしか動いていないのです。あとはバレルから飛び出すまで空気の膨張のみの力で弾は加速してゆきます。PDWの場合10.6msで飛び出して行きます。
次にピストンと弾の速度について見てみます。

ピストンの速度は穴位置を越えるまで当然のように加速し続け、穴位置を超えてからは急速に減速します。これはスプリングの押す力は逆比例で弱くなりどんどん圧縮された空気によって減速しています。
ちなみにPDWの場合ピストンがピストンヘッドに衝突する時の速度はたかだか2.6m/s（時速9.4km）ですのでピストンヘッドの衝撃吸収材を変えたところでたいした効果は無いのではないでしょうか？弾がないと減速しませんので11.2m/s（時速40.3km）で衝突します。これは結構な速度です。あんまり空撃ちを繰返すと確かにおかしくなりそうです。
最終的に弾速度は110m/sでバレルから飛び出して行きます。現実には70～80m/s程度なのでやはり空気の漏れ量くらいは考慮に入れる必要があるのでしょう。
この辺くらいで最適な条件がうっすらと見えてきました。ピストン後退端のエネルギーは穴位置やシリンダ質量に関係なくスプリングのポテンシャルエネルギーのみであるので、ピストン前進端に達する瞬間のピストン運動エネルギーを最低にすればその差が弾に与えられるエネルギーになります。
ただしあまりピストンを軽くしてしまうとピストンスピードが上がり、圧力が急上昇して逆にピストンが押し戻される条件もあり得ます。この場合はせっかく与えたエネルギーがピストンに戻され大幅に弾速度が落ちてしまいます。さらにピストンが前進端に落ち着く時間も遅くなってしまいますのでハイサイクルを狙う場合注意が必要です。
2004/3/25